対数の計算法則の使い所 対数は多くの学生が苦手とするところですが、その大きな要因の1つがこれら 計算公式の乱用 です。 定義も考えず、ただ公式に当てはめるだけのパズルゲームにした途端、対数はその魅力を全て失います。 例えば、以下 lim と書けば、 lim n→∞のことであるとします。極限の足し算の公式(?) lim(a_n),lim(b_n)が存在するとき、\(\arg\) や \(\log\) の足し算や掛け算は通常の数に対する演算ではないため注意が必要となる(ただし集合の要素の1つ1つに対しては通常の足し算や掛け算を行っている)。 指数法則\eqref{exp}は、底が \(e\) でない一般の場合には注意が必要となる。

Log同士の足し算ってかけ算になって Log同士の引き算って割り算になりますか Clear
Log 足し算 掛け算
Log 足し算 掛け算-偶関数と奇関数の意味,性質などまとめ レベル ★ 基礎 いろんな関数 更新日時 偶関数と奇関数の定義,意味,見分け方,性質を解説します。 グラフを描いたり定積分の計算に役立つ考え方です。 目次 偶関数の定義,見分け方 奇関数の定義 logの真数が掛け算で表されていたらそれぞれ足し算に 分けることができ、 真数が割り算で表されていたらそれぞれ引き算に 直すことができます。 証明は省略しますが、対数の計算などで非常によく出てくるので確実に押さえましょう! ⑦




ট ইট র Norihito4 昨日録画した Bsキャンパスon 数学の歴史 第10回 対数から積分法へ を視聴 待ってました 計算尺 の登場 ヘンミno 2664sを使用し 掛け算を対数目盛による距離の足し算で表していることを解説 2 3 6 を Log 2 Log 3 Log
右のコードエリアには、足し算をおこなうプログラムがあります。このプログラムを修正して、以下の掛け算をおこない、計算結果を表示してください。 * 67 採点ボタンをクリックして、正解と表示されれば演習課題クリアです!足し算がかけ算に等しいということではない. log a Mlog a N ←#等しくない#→ log a M log a N 「2つの対数の和」は「真数の積の対数」に等しいということ log a Mlog a N ← 等しい → log a MN 対数のメリットは「掛け算を指数の足し算に変換できること」だと思って大丈夫です。 対数を使って指数法則を一般化する 先ほどの具体例を一般化すると log10(A * B) = log10A log10B になります。
P=0 p = 0 とすれば5を得る。 ( a 0 = 1 a^0=1 a0 = 1 であることから直接分かる,この方が素直) なお,6については 底の変換公式の証明と例題 で詳しく解説しています。 1~6を使えばほとんどの対数の計算問題を突破できますが, 覚えておくと便利な対数の統計学的画像再構成法である OSEM アルゴリズムの基礎論 第1章 確率・統計の基礎 1.1 シグマ(Σ)とパイ(Π)と対数( Log )の記号 さて、平均値をもう少し詳しく記号で見てみましょう。「平均なんて簡単だよ!対数方程式の変形例 log 2 xlog 2 (x1)=1 → log 2 x (x1)=log 2 2 (例外) 「log 5 18をlog 5 2とlog 5 3で表せ」というような問題では「分ける」方向で変形しますが、高校生が出会う問題の中ではわずかな量です。 ※対数の歴史から言えば、かけ算、割り算(累乗)の
パッと見た感じ、logを使うようには見えないんだけど 今回の関数を微分するためには対数微分法というやり方を用います。 まずは、底\(e\)とする対数を両辺にとります。 $$\log y=\log x^x$$ $$\log y=x\log x$$ ここから両辺を微分すると $$\frac{y'}{y}=\log x1$$(例)BASICで log 10 2 を計算する場合,log 10 2 = log e 2 ÷ log e 10 だから,計算式は Log(2)/Log(10) とすればよい。 また,eを底にした指数関数には微分について以下のような性質がある。 (e x)' = e x (補注:(a x)' = a x × log e a 指数を前に出すと,\ 対数は\log_25のみになる \\2zh こうして各括弧内で和が計算できるようになり,\ 最終的に対数は約分で消える まずは底を10に統一する\ \ a,\ bで表すには,\ 真数が素数になるまで分解する \\2zh 結局,\ \log_{10}5を求めることに帰着する




これの解き方教えてください 答えしか載ってなくてよくわからないです Clear




と の疑問です は対数の性質で足し算を掛け算にまとめていますが 数学 教えて Goo
1.足し算(引き算)の時は、小数点以下のケタ数のもっとも少ない数に揃えて計算する。 例:563 0574 = 563 057 = 6 2.掛け算(割り算)の時は、有効ケタ数を揃えて計算する。 一般社団法人村楽 地域おこしにおける「足し算の支援」と「掛け算の支援」は、明治大学・小田切徳美先生が提唱する誇りの再生のプロセスです。 「この地域はどうせ寂れていくだけだ」「何をやってもしょうがない」というネガティブ 数学Ⅱ 対数同士の引き算で、三つ以上の時のやり方がどうなるのか分かりません。 3log5 12 log5 300 2log5 60 この式を整理すると log5 12^3 log5 300 log5 60^2 ここまでは分かるのですが、計算していくと log5 (1728/300/3600) = log5 という結果になってしまい、




Logの計算ができません 囲ってあるところがどうして Clear




対数とは何なのかとその公式 メリットについて 対数をとるとはどういう意味か アタリマエ
Deg / Rad log ln % BACK sin cos tan 7 8 9 ÷ sin1 cos1 tan1 4 5 6 × x y x 3 x 2 1 2 3 – y √x 3 √x √x 0 = e x e π x ± Ans AC EXP 1/x 10 x n!では,なぜこの表で掛け算,割り算が出来るのでしょうか。①の計算で説明すると, log 10 32log 10 15=log 10 (32×15)=log 10 48 が成り立つことで分かってもらえるでしょう。そう,対数をとると,掛け算は足し算に変わるんでしたね。 これは今証明した1つ目の性質を使えば証明できます。対数の足し算は真数の掛け算でしたので、それを逆に使いましょう。 どういうことかというと $$\log_{a} b^{c}$$ という式はこう考えることもできます。 $$\log_{a} b^{c}=\log_{a} (b\times b\times \cdots \times b)$$




一刀両断 Logが Phへと導かれる仕組み 夢のバケ学




世界は足し算でできている 古代ギリシャからコンピューターまで 桜井 進 本 通販 Amazon
Log(24 x 105) = log 24 log105 = log 24 5 = 指標はそれぞれ3,4,5であり,有効数字ではない.仮数はいずれも log 24 = である.ここで,真数の有効数字は2桁であるので,対数はそれぞれ338,438,538 となる. Title使い方も分かりやすく、簡単に計算できて非常に助かります! アンケートにご協力頂き有り難うございました。 送信を完了しました。 対数関数 のアンケート記入欄 性別 男 女 年齢 歳未満 歳代 30歳代 40歳代 50歳代 60歳以上 職業 一刀両断! logが、pHへと導かれる仕組み! ? こちらでは、 pH (水素イオン指数)へと導くために、不可欠な常用対数の基礎について記載してあります。 更に、常用対数に関連のある指数等を交えながら、基礎的pHを理解していきましょう。 また、pH計算に




掛け算を足し算で考える ログ Log キソカラ



対数の計算
定義 対数は次のように定義され、記号 log を用いて表されます。 M = ap (a ≠ 1, a > 0, M > 0) M = a p ( a ≠ 1, a > 0, M > 0) という関係があるとき、 p p を a a を底(てい)とする M M の対数といい、 p = loga M p = log a M と表す。 M M を 対数 p p の真数という。 この 簡単な演算子を使って計算してみよう みなさまどうも。 いかがお過ごしでしょうか。 引き続き簡単な『 演算子 』を使って計算をしてみましょう。 演算子とは演算に使用する記号の事を指します。 『』とか『』とかのことです。 演算子は色々な種類Logの計算 ここでは、logを使った計算の法則について学んでみましょう。 まず、logには以下の法則があります。 掛け算はlog同士の足し算 割り算はlog同士の引き算 n乗はlogの前に出すこ



1



底の変換公式
MM MR できること 足し算、引き算、掛け算、割り算、指数、平方根、対数、三角関数などの計算ができます。 足し算、引き算、割り算、、、、、とか、もう、数えきれない。 そんななかに、 ルートの掛け算の計算 がある。 ルートの掛け算の基本は、 ルートの中身を掛け算するだけ だったよね?? そんなむずくなさそう。 だけどね、実際の計算問題だとそうは 「何回微積分しても変わらない」というのは、意味合い的には加法(足し算)においては $0$ 、乗法(掛け算)においては $1$ で、どちらも相手を変化させないですよね。 $\log_{e}x$ の使



Logの計算するとき Logの足し算は掛け算になりますが Lo Yahoo 知恵袋



Logの足し算 引き算についてです Logの底と真数が同じ Yahoo 知恵袋
logの問題についてですlogの底が同じだと足し算→掛け算・引き算→割り算になって底が違うと足し算引き算そのままに計算するでいいんですか? 高校 解決済 教えて!goo



Logどうしの掛け算の方法を教えてください 一般的に言えば Lo Yahoo 知恵袋
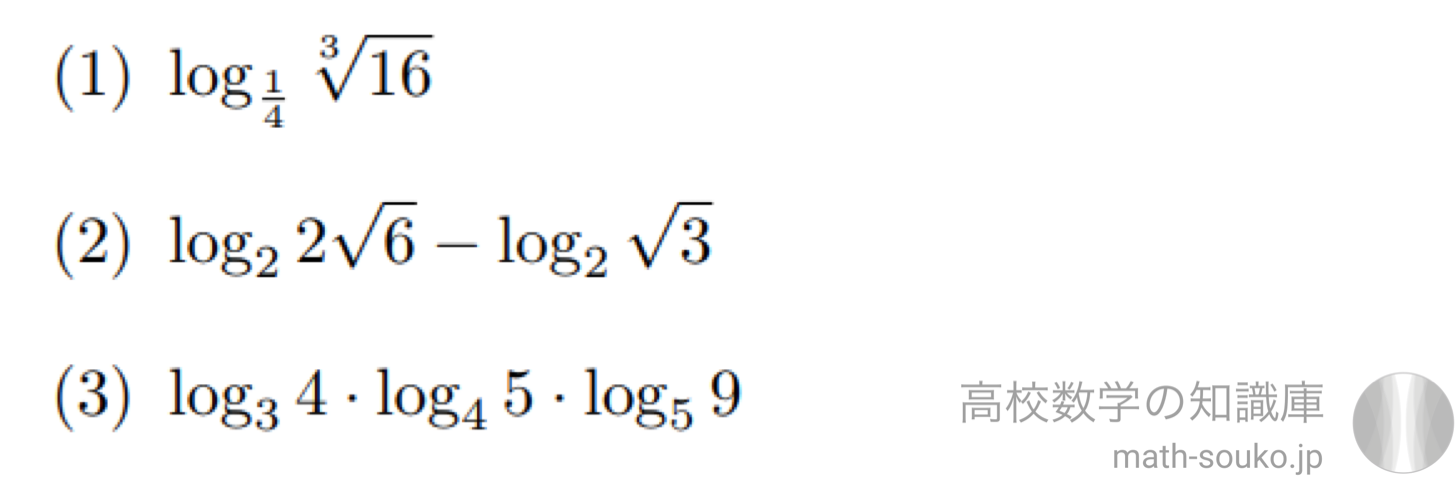



対数法則を使う対数計算の問題 高校数学の知識庫




対数 Log の計算と公式 これでもうバッチリ Kenブログ 風のように しなやかに




文系のためのめっちゃやさしい 対数 ニュートンプレス




対数関数とは Logの基礎から公式やグラフまで解説 高校生向け受験応援メディア 受験のミカタ
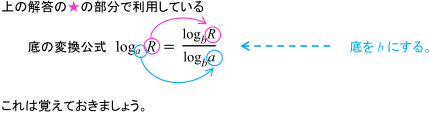



底をそろえて計算するときの底の決め方 数学 苦手解決q A 進研ゼミ高校講座



緊急です 数iiの問題で Logの足し算は掛け算にすると教わ Yahoo 知恵袋




赤いマーカー部分のlogの計算は足し算なので掛け算するのでは無いのですか Clear




ট ইট র Norihito4 昨日録画した Bsキャンパスon 数学の歴史 第10回 対数から積分法へ を視聴 待ってました 計算尺 の登場 ヘンミno 2664sを使用し 掛け算を対数目盛による距離の足し算で表していることを解説 2 3 6 を Log 2 Log 3 Log
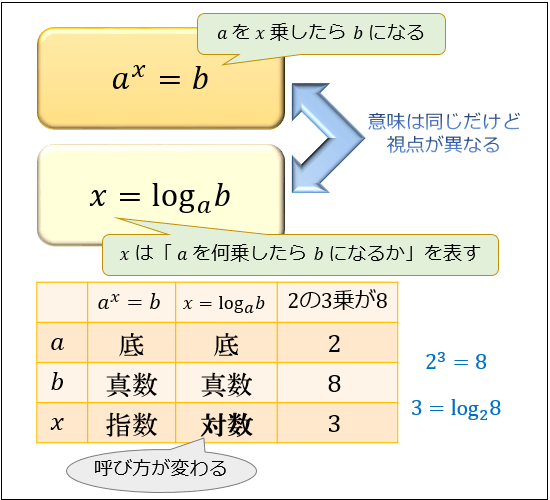



対数とは何なのかとその公式 メリットについて 対数をとるとはどういう意味か アタリマエ



指数関数 計算 足し算
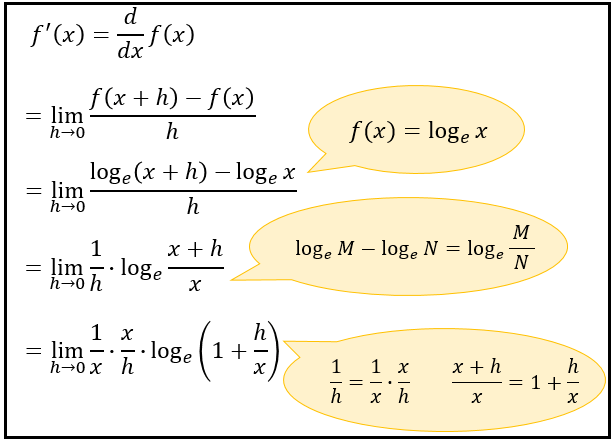



自然対数 Log X の微分公式について 導関数の定義式と意味から分かる証明方法 アタリマエ



Logの足し算 引き算についてです Logの底と真数が同じ Yahoo 知恵袋
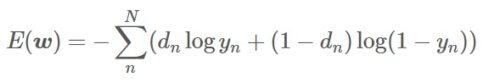



対数で掛け算を足し算に変換 対数の2つのメリットを解説



数学用語解説 数 指数関数と対数関数




ট ইট র Norihito4 昨日録画した Bsキャンパスon 数学の歴史 第10回 対数から積分法へ を視聴 待ってました 計算尺 の登場 ヘンミno 2664sを使用し 掛け算を対数目盛による距離の足し算で表していることを解説 2 3 6 を Log 2 Log 3 Log



Logの足し算はlogの前の係数を合わせてからしかできませんか まぁ Yahoo 知恵袋




指数 対数関数の公式 指数法則と対数法則と底の変換公式の証明 Irohabook
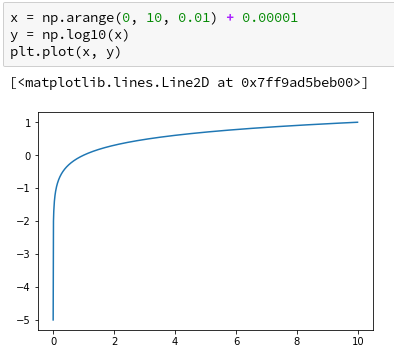



今度こそ分かる 対数関数 Log関数 Qiita




数学 対数関数 対数の計算 オンライン無料塾 ターンナップ




Log同士の足し算ってかけ算になって Log同士の引き算って割り算になりますか Clear



Q Tbn And9gcsmzu4yxdpscnm9nk3sp3ko0 Ag8sahcn Bnp1x19yodulopepg Usqp Cau




なぜ上はlog同士を足し算 引き算しているのに対し Clear




この 1 の計算 普通に掛け算して消していってるのですが なんかlogの掛け算は足し Clear



Logの計算について質問です Logの足し算は掛け算にすると Yahoo 知恵袋



底の変換公式
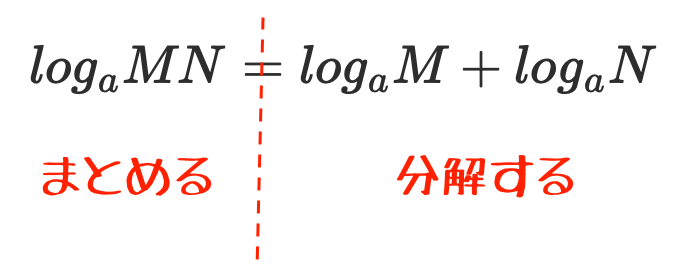



対数の計算法則 なぜ掛け算が足し算に 対数の計算は定義を見返そう 青春マスマティック




掛け算を足し算で考える ログ Log キソカラ
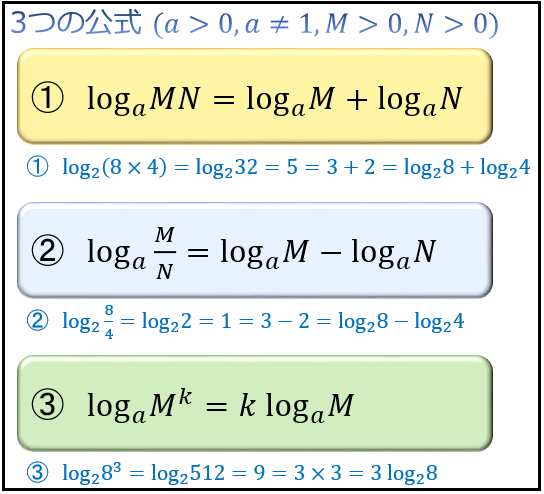



対数とは何なのかとその公式 メリットについて 対数をとるとはどういう意味か アタリマエ




高校数学 底の変換公式 練習編 映像授業のtry It トライイット
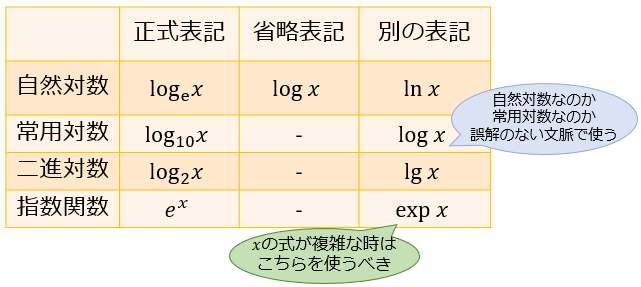



自然対数 常用対数 二進対数の使い分け Log Ln Lg Expはどういう意味 アタリマエ




対数関数 Log で1カ月悩んだ高校生が15分の解説でスッキリした話し マナビバ ー 個別指導ヒーローズから始める学びのポータルサイト
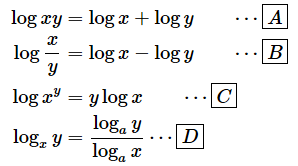



Ai 機械学習の数学 番外編3 指数と対数 対数編 Ai 機械学習の数学入門 It
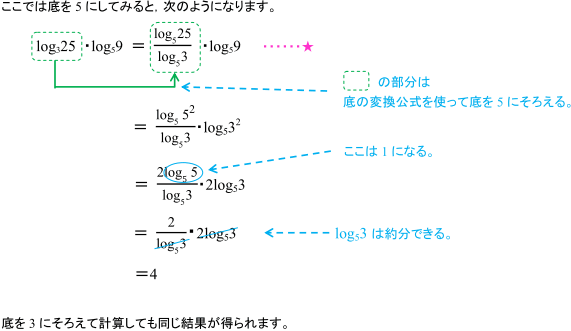



底をそろえて計算するときの底の決め方 数学 苦手解決q A 進研ゼミ高校講座




高校数学 底の変換公式と対数の性質による対数の基本計算 受験の月




対数で掛け算を足し算に変換 対数の2つのメリットを解説
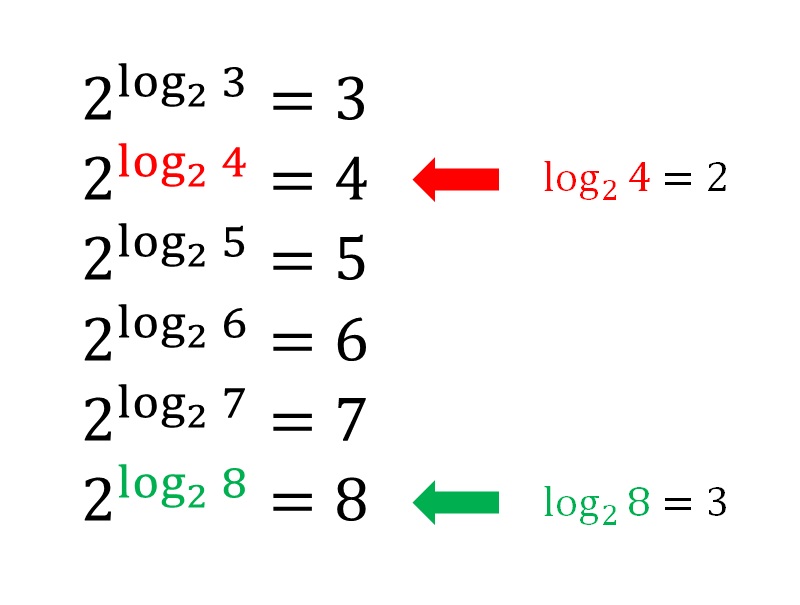



Log 対数 とは何なのか 感覚でカンタンに高校数学




累乗の逆 むかし数学で習った 対数 を超やさしく解説 Log



対数の計算




Javascript 初級編1



対数について 計測制御 Labview徒然草 By 成田義也




ぱせり こんなやつなんで足し算 引き算 掛け算 割り算16問ずつあるん 4問ぐらいでええやん




と の疑問です は対数の性質で足し算を掛け算にまとめていますが 数学 教えて Goo
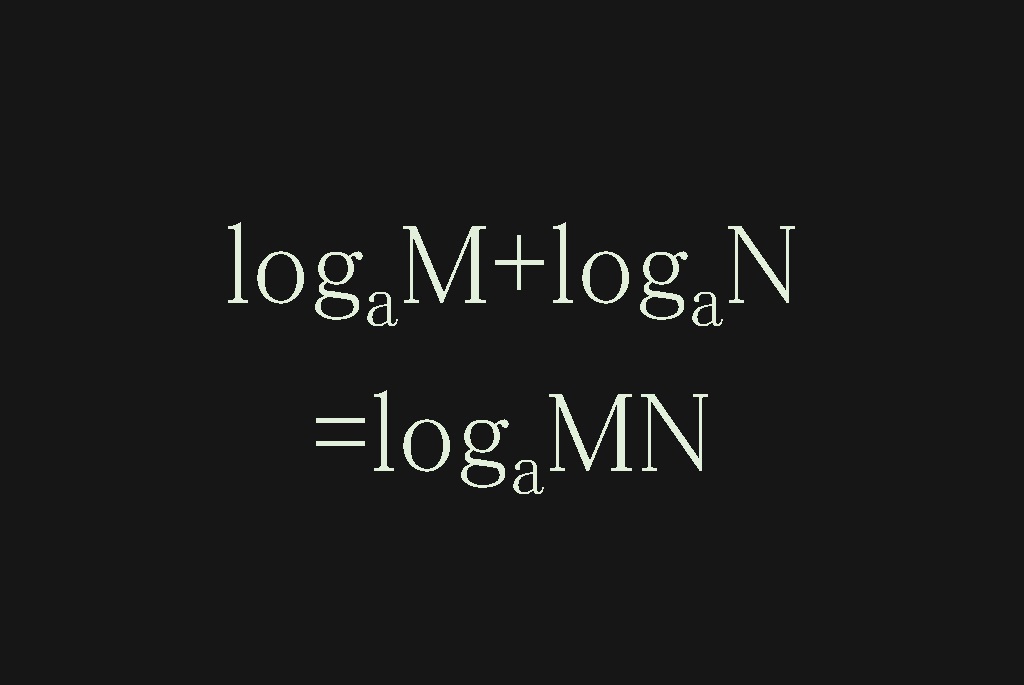



対数の性質と計算ルール 統計学が わかった



Log Log 尺のなぞ




Log ログ って何 常用対数 自然対数とは 対数を徹底解説 青春マスマティック




丸がついている部分 なぜlogが同じだったらかけ算に 直すのに直さず 高校 教えて Goo




対数 Log の計算と公式 これでもうバッチリ Kenブログ 風のように しなやかに




Je6tor Jn6uae Logを用いない 簡単db 真数計算法 3db 2 3db 2 10db 10 10db 10 これを基本形にして ひたすらdbを足し算か引き算にし それを真数の掛け算か割り算に換算し 真数を求める という方法で 一陸特や1アマまでなら十分




指数 対数関数の公式 指数法則と対数法則と底の変換公式の証明 Irohabook



Logの足し算 引き算についてです Logの底と真数が同じ Yahoo 知恵袋




これの解き方教えてください 答えしか載ってなくてよくわからないです Clear




対数 Log の計算と公式 これでもうバッチリ Kenブログ 風のように しなやかに




下線部のところなんですけどlogって足し算はかけるんじゃないんですか Clear




対数関数とは Logの基礎から公式やグラフまで解説 高校生向け受験応援メディア 受験のミカタ



底も真数も同じ対数の掛け算ってどうやって計算しますか 図のような計算って Yahoo 知恵袋




Aeton この2日間で取り組んだ数学研究 初等巨大数研究の一環で ただの足し算をあえて掛け算 累乗 対数で近似表現する試み おこじょ数の基礎を成す演算でもある 色々やってみた結果 Eの凄さを目の当たりにすることに



掛け算と足し算 Log Of Roygb



掛け算 を 足し算 で 計算 計算尺 Bar Soryu Shi



3




イメージでわかる冴子先生の高校数学 対数log編 数学はこちら 漫画で表してます Manabi100



1




指数 対数関数の公式 指数法則と対数法則と底の変換公式の証明 Irohabook




数 足し算 引き算 掛け算 割り算 不等式の英語表現を覚えよう ゆう アメリカ生活終了 英語勉強




祥太 7 25ロズガ か6 Showtime בטוויטר 昔の人の知恵の結晶 計算尺 ざっくり説明すると リニアスケールでの掛け算がログ スケールでは足し算になることを応用し 乗除算や指数対数三角関数などを電卓なしで計算できてしまう優れた道具なのです




掛け算を足し算で考える ログ Log キソカラ




対数とは Logって何 対数関数について基礎から解説 高校生向け受験応援メディア 受験のミカタ




対数の足し算は真数の掛け算 ゼロからわかる対数その2 Youtube
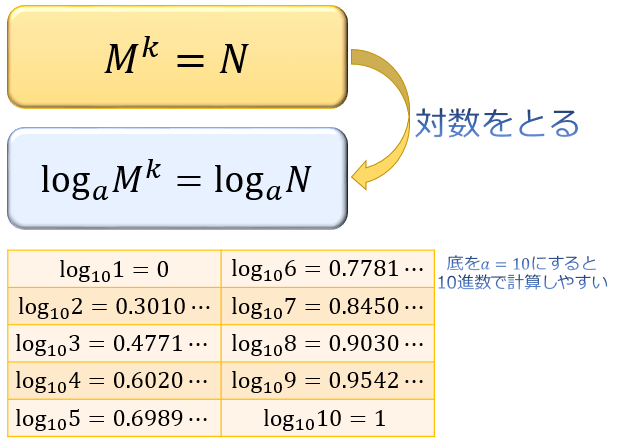



対数とは何なのかとその公式 メリットについて 対数をとるとはどういう意味か アタリマエ




Aeton この2日間で取り組んだ数学研究 初等巨大数研究の一環で ただの足し算をあえて掛け算 累乗 対数で近似表現する試み おこじょ数の基礎を成す演算でもある 色々やってみた結果 Eの凄さを目の当たりにすることに



対数は 震度にも 音楽にも 理科のphにも使われている




対数の加法と減法 対数関数 数学の部屋



統計学的画像再構成法である
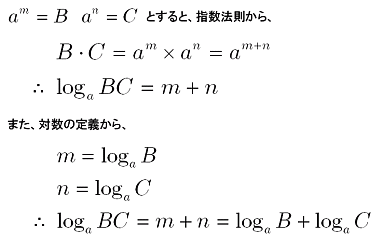



対数 対数の計算公式 大人が学び直す数学




対数とは Logって何 対数関数について基礎から解説 高校生向け受験応援メディア 受験のミカタ




対数の計算法則 なぜ掛け算が足し算に 対数の計算は定義を見返そう 青春マスマティック



Logの足し算 引き算についてです Logの底と真数が同じ Yahoo 知恵袋
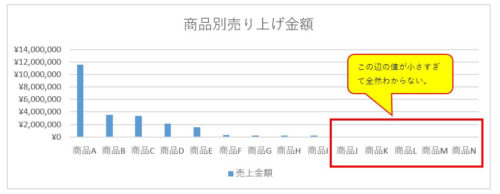



対数で掛け算を足し算に変換 対数の2つのメリットを解説




対数で掛け算を足し算に変換 対数の2つのメリットを解説



第5回 演算子の使い方を学ぶ Unityで学ぶc 入門 Xr Hub



Logの足し算はlogの前の係数を合わせてからしかできませんか まぁ Yahoo 知恵袋




対数とは Logって何 対数関数について基礎から解説 高校生向け受験応援メディア 受験のミカタ



対数の計算は足し算は真数の掛け算になって引き算は真数の割り算になると思うんで Yahoo 知恵袋




指数 対数関数の公式 指数法則と対数法則と底の変換公式の証明 Irohabook




計算のスピードアップ コンピュータでも Sin Cosの計算は大変です 足し算 引き算 掛け算 割り算は早いです Ppt Video Online Download



対数表




対数とは Logって何 対数関数について基礎から解説 高校生向け受験応援メディア 受験のミカタ



常用対数




Logの足し算は掛け算で計算するのじゃないんですか なぜここは通分なんですか Clear
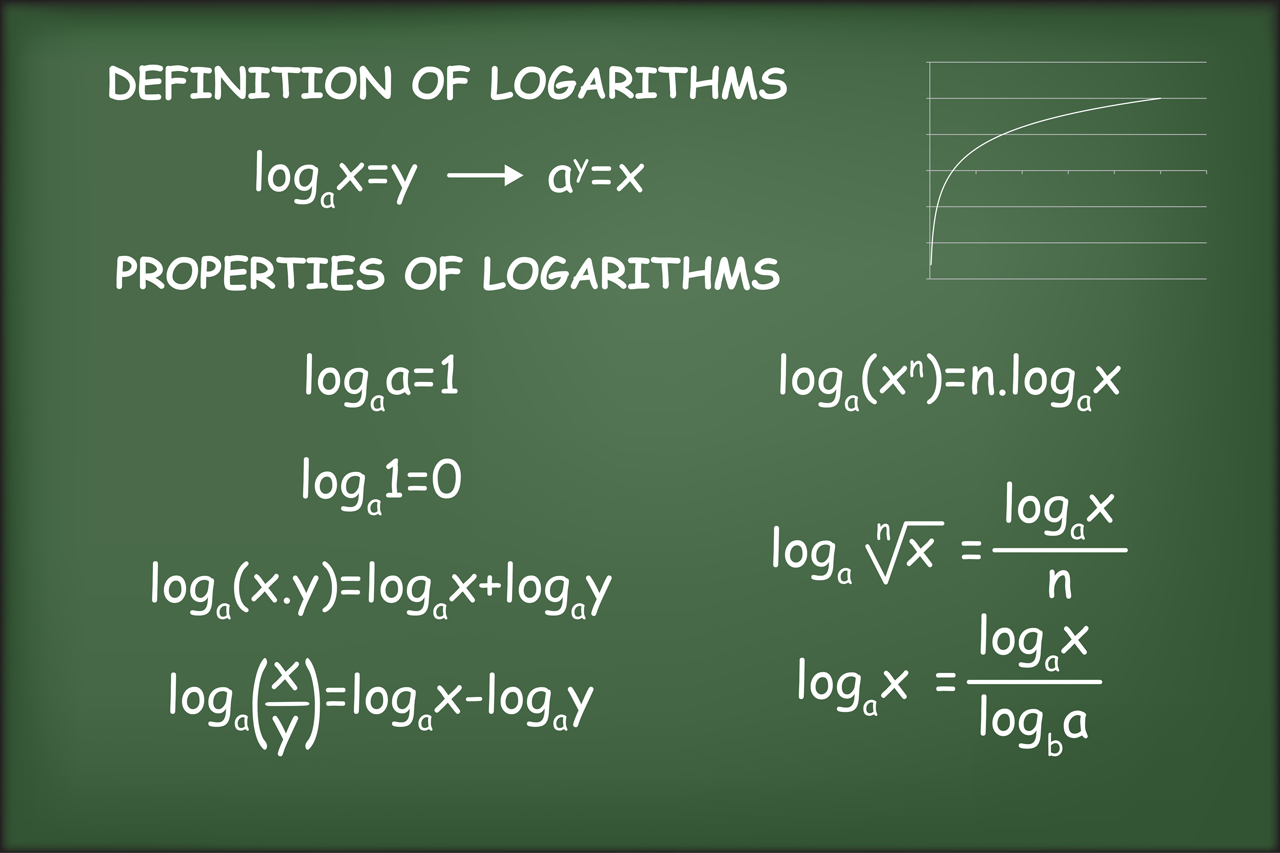



Ai 機械学習の数学 番外編3 指数と対数 対数編 Ai 機械学習の数学入門 It
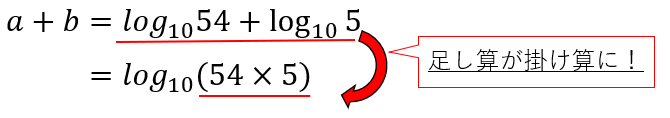



掛け算を足し算で考える ログ Log キソカラ




対数関数 Logの意味と頻出公式まとめ 底の変換公式と裏ワザも紹介 ますますmathが好きになる 魔法の数学ノート



0 件のコメント:
コメントを投稿